Category: Energy

The Eco-Cooler for Free Air Conditioning

Screenshot

Today we explore a completely passive air conditioner with no moving parts. You may have heard of it. It’s called the Eco-Cooler and it was invented by Ashis Paul, a Bangladeshi innovator.

In 2016, news outlets around the world reported on his creation of a low-cost, electricity-free air conditioner made from recycled plastic bottles. This design aimed to help people in rural Bangladesh cope with the sweltering summer heat, especially those living in homes with limited access to electricity.

The Bernoulli principle and the ideal gas law are the two fundamental principles at play in air conditioners. In theory, an Eco-Cooler functions on the same principles as any compressor driven A/C unit.

The Bernoulli principle states that for an incompressible fluid (like air) flowing in a horizontal stream, an increase in the speed of the fluid is accompanied by a decrease in its pressure. This means as air flows faster, it experiences a drop in pressure. This speed and pressure change is created in the Eco-Cooler as the air stream is forced through the much smaller opening of the bottle neck, causing it to speed up.

The ideal gas law describes the relationship between pressure, volume, and temperature of a gas. According to the ideal gas law, this lower pressure causes the air stream to get hotter by what’s known as adiabatic heating. If this heat can be removed, the air will be chilled upon expansion.

In essence, Bernoulli’s principle creates the pressure differential that drives the heat transfer process in air conditioners, and the ideal gas law explains how this pressure change affects the temperature of the faster moving gas (air in the case of the Eco-Cooler). This interplay of principles is essential for achieving the cooling effect in air conditioners.

I have a treat for you today. I finally took the time to sit down and work out all the engineering behind this simple design.

Here’s what I came up with:

Eco-Cooler, 2L Bottle

Assumptions:
Air speed: v₁ = 2.5 mph (1.12 m/s)
Air pressure: P₁ = 1 atm = 101,325 Pa
Air temp: T₁ = 40°C (313.15°K)
Air density: ρ = 1.225 kg/m³
Specific heat ratio, Cp/Cv: ɣ = 1.4

Given:
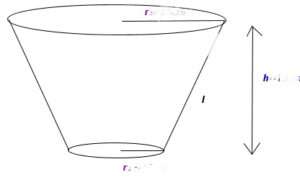
D₁ = 4.25” (11 cm)
D₂ = 0.5” (1.27 cm)

Calculate Areas:
A₁ = 𝛑(11/2)² = 95 cm²
A₂ = 𝛑(1.27/2)² = 1.267 cm²

Calculate velocities:
By the continuity formula…
A₁v₁ = A₂v₂
v₁ = 1.12 m/s
v₂ = 95•1.12/1.267 = 84 m/s

Calculate pressures:
ΔP = 0.5 ρ(v₂²-v₁²)
= 0.5•1.225•(84²-1.12²)
= 4,321 Pa
P₁ = 101,325 Pa
P₂ = P₁ + ΔP
P₂ =101,325+4,321 =105,646 Pa
P₂/P₁ = 1.043

Calculate Temperatures:
T₂ = T₁ (P₂/P₁)^((ɣ-1)/ɣ)
= 313.15•(1.043)^(0.4/1.4)
= 316.9°K
= 43.8°C

(As a result of radiative cooling)
T₂ => 313.15°K

After expansion
T₃ = T₂ (P₁/P₂)^((ɣ-1)/ɣ)
= 313.15•(1/1.043)^(0.4/1.4)
= 309.4°K
= 36.3°C
= 97.34°F (down from 104°F)

And there you have it ladies and gentlemen. This is how the Eco-Cooler is supposed to work. However…

The Eco-Cooler, while innovative in its concept of a passive cooling solution, has a mixed reputation. You will find lots of YouTube video reviews online and virtually every one of them claims that it doesn’t work.

I think it’s clear why. In the design, as described, there is literally no means by which to remove the excess heat energy. You must cool the compressed air before allowing it to expand again if you want satisfactory results. Isn’t that how your standard compressor operated A/C unit works? Of course it is.

The faster moving air at the outlet may help increase evaporative cooling effects but that wasn’t the purpose for its compression in this design. It makes absolutely no sense to immediately allow the hot air to re-expand without having removed excess heat energy from it first.

The addition of heat radiating fins to a pipe of increased length would give this thing a fighting chance. The longer path would provide additional time to carry out the heat transfer. In extreme cases it may even be necessary to use a water bath to carry off that excess heat. Yes, this would add expense and complexity but the dividends in performance should be well worth it.

Eco-Cooler Summary

So, to summarize then,

Pros

Low Cost and Simple Design: Made from recycled materials like plastic bottles, the eco-cooler is very inexpensive to build. It doesn’t require electricity, making it suitable for off-grid locations.

Passive Cooling: The design utilizes the Bernoulli principle for a passive cooling effect, offering an alternative to energy-intensive air conditioners.

Environmental Benefits: By using recycled materials and avoiding electricity, the eco-cooler has potential environmental benefits.

Cons

Limited Cooling Capacity: In its basic form, the eco-cooler’s cooling effect is relatively weak and may not be sufficient for significant temperature reduction, especially in hot climates.

Real-World Limitations: Factors like friction and imperfect heat transfer can hinder the effectiveness of the cooling process.

Need for Improvement: The basic design requires modifications like pre-cooling with radiator fins to achieve a more noticeable cooling effect.

A Time for Reflection

Let’s consider a new machine with no moving parts… a mirror. Oh. You say you’re not sure a mirror qualifies as a machine?

Well, OK then. Let’s make the mirror part of a solar oven. Feel better now? LOL

With that out of the way, let’s say we have a spherical oven with a round opening to receive solar energy. What would it take to create a light collecting mirror that would maximize the amount of energy directed into our oven? Obviously, we need a wide opening at the top. The wider the better, right? And the angle of the mirror should be such that every ray of light that strikes the mirror is reflected into our oven.

Waste not, want not, I always say. Before we leave that thought, can we agree that a rectangular setup of four flat mirrors, although easy to make, cannot meet our requirements since the surfaces near the corners reflect at sub optimal angles.

Break It Down For Me

Well, we must conclude that in order to maximize the collection of solar energy fed into a circular opening, we need a conical funnel, technically called a frustum, designed with the following characteristics:

  • Area:

    The area at the top of the funnel must be large enough to capture all the energy required for our design. Solar insolation is generally taken to be 1000 watts per square meter. Good to know.

  • Funnel angle:

    Funnel angle is the angle between the slant side of the funnel and the vertical axis. This is actually called the ‘half-angle’ since there is a duplicate on the other side. It is typically measured in degrees. While it is true that a wider funnel angle will increase the projected area of the funnel’s opening, we already know the area required to accept the amount of sunlight that is to be collected. The angle must be chosen to assure that all the captured light is actually directed into the opening we are trying to target. Although it may look strange, the formula for this angle is:

    Ø = ½cos⁻¹(½(D/d-1))

    Where:
    D is the large diameter at the top and
    d is the smaller bottom diameter

    • Important note: If D/d is 3 or greater, this formula will fail. You must either reduce your large diameter or increase the small one. Ratios of 3 or more require infeasibly small angles. Like, you know? Straight up. That’s no good. LOL. So, watch your selection of D and d values. Oh, and smaller ratios will produce shorter solar funnels. That calculation is the next step.

  • Funnel height:

    The height of the funnel is chosen in coordination with the two diameters to achieve the desired angle. The formula is:

    Height = (D-d)/(2tan Ø)

    Where the variables have been previously defined.

  • Sun angle:

    The funnel should be oriented so that the angle of incidence of sunlight is as close to 90° as possible. This simply means it needs to be pointed directly at the sun if we want to ensure that the maximum amount of sunlight is collected. Surprise! Duh.

Show Me An Example

Ok, for example, we might decide we want to design a 650 watt solar oven. To achieve this would require an area of 0.650 m² at the top of our funnel given the normal amount of solar radiation that reaches us on a sunny day. We can make the following calculation:

D = 2*sqrt(0.650/𝛑) = 0.91 m or 36”

Let’s suppose we decide that a 14” diameter opening is a suitable size to feed our oven. We can now derive the proper funnel angle:

Ø = ½cos⁻¹(½(36/14-1)) = 19.1°

And finally, the height must be:

H = (36-14)/(2*tan(19.1)) = 31.77”

You can check your work by testing this relationship:

(D-d)/(D+d) = tan Ø/tan 2Ø

All that remains is to make a flat pattern to fabricate our funnel. There is a nice calculator available here. It even tells you the size of the sheet material you will need. That material must be as smooth as possible with a mirror finish. Any imperfections will reflect light in directions not consistent with our goal.

Crinkled aluminum foil is probably not the best answer you could come up with. Aluminuzed mylar will probably work for a while. Be aware however, the aluminum will slowly oxidize over time and the alumina (aluminum oxide) will flake off. This is unfortunate indeed.

Explain The Theory Behind Your Numbers

Sure. We are assuming that the solar rays of light are parallel and enter the funnel straight on, that is, we are pointed directly at the sun and perfectly aligned. Any rays coming in without touching the reflector simply enter straight into our oven. In practice, without a functioning tracker device, this won’t be true but we must start somewhere.

We know from physics that the angle of reflection equals the angle of incidence. Our reflector angle must be such that it will map every incoming incident ray across the entire opening. What this means is that a ray that strikes the middle of the reflector must enter the oven through the center of the opening. One that just manages to strike the reflector at the bottom edge must enter right near there while one that catches the top of the reflector must be deflected all the way across the space to enter at the other side. All reflected rays are in parallel as they enter the oven opening.

The angle formula given above does exactly this. In order to achieve this optimal angle, we must adjust the height of our funnel. This is essentially the equivalent of focusing. By adjusting the height we can focus the incoming light to exactly match the size of our opening, thus maximizing the input energy.

So, there you have it. It looks like you got a two-fer with this post. We set out to explore mirrors as machines with no moving parts and learned something about solar ovens in the process. We aim to please. Enjoy.

Bonus2: Another pattern calculator.